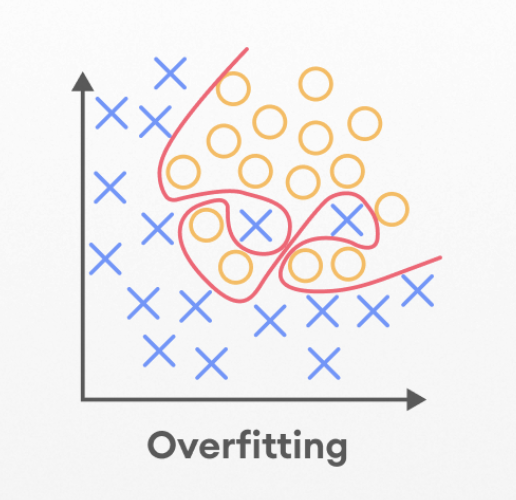
Machine learning algorithms are designed to learn patterns from a dataset and make predictions based on those patterns. If an algorithm is trained on a dataset that has too much noise, it may develop a model that is not able to generalize well to new data. This is known as overfitting.
One way (not the only one) in which overfitting can occur is when an algorithm is trained on completely random data. Because random data does not contain any inherent patterns, a model trained on such data is likely to develop a representation that does not correspond to any real underlying pattern in the data.
For example, let’s say we have a dataset with 100 data points that are completely random, with no relationship or correlation between the features. We train a regression model on this data, assuming that the data has a linear relationship. As the model will try to fit a line that goes through every point, the model will be highly complex, with many unnecessary degrees of freedom. This model will not perform well when applied to new data. Example:
In addition, when the model is trained on completely random data, the training error will be low, as the model will be able to fit to the training data exactly, but the test error will be high, as it will not be able to generalize well. This mismatch in performance between the training and testing data is a key indication of overfitting.
Another example of this phenomenon can be seen in decision tree algorithms. Decision trees are constructed by recursively partitioning the data into smaller subsets based on certain conditions. When the data is random and does not contain any underlying patterns, the decision tree may end up creating a large number of branches, each corresponding to a specific subset of the data, resulting in a model that is highly complex and not able to generalize well to new data. Example:

To combat overfitting, a common technique is to use regularization, which penalizes models that are too complex, or to use cross-validation to evaluate the model’s performance on unseen data. Another approach is to increase the size of the dataset to reduce the noise and to make sure that the model is exposed to a wide variety of data. Additionally it’s important to always keep track of performance metrics like precision, recall, accuracy, and F1-score and not only focus on the training error.
CODE EXAMPLE:
Random dataset¶
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier
nrows, ncols = 1000, 2
features = ['x'+str(i) for i in range(ncols)]
df = pd.DataFrame(np.random.randn(nrows, ncols), columns=features)
df['y'] = np.random.choice(["yes", "no"], size=nrows)
df.head()
| x0 | x1 | y | |
|---|---|---|---|
| 0 | 1.021167 | -1.111160 | no |
| 1 | 0.677099 | 0.847936 | yes |
| 2 | 0.702123 | -0.244699 | yes |
| 3 | -0.100375 | 0.022832 | yes |
| 4 | 0.492049 | -0.122740 | no |
fit and predict¶
model = RandomForestClassifier(n_estimators=100)
model.fit(df[features], df['y'])
predictions = model.predict(df[features])
pd.crosstab(df['y'], predictions, rownames=['actual'], colnames=['predicted'])
| predicted | no | yes |
|---|---|---|
| actual | ||
| no | 493 | 0 |
| yes | 0 | 507 |